MCMC for dummies
학부 확률과정론 시간에 교수님께서 MCMC를 열성적으로 강의하셨지만 학생들이 너무 멘붕에 빠져서 결국 시험범위에서는 제외되었던 기억이 난다. 그것이 mcmc에 대한 첫 인상이었는데, 졸업까지 총 세 과목에서 공부했지만 제대로 공부하지 않고 항상 피해다니려고만 했다. 그리고 결국 다시 공부를 해야하지 않을까 하는 생각이 마구마구 든다. 이럴거면 미리 잘 해둘걸….
아무래도 수식보다는 절차가 잘 설명되어있는 코드를 직접 돌려보면서 공부하는 것이 좋을 것 같아서 관련 글을 검색해보기 시작했다. 그러다 찾아낸 http://twiecki.github.io/blog/2015/11/10/mcmc-sampling/ 을 보고 해당 글의 내용을 R로 옮겨서 작성해봐야겠다는 생각이 들었다. 포스팅 후반부의 시각화 부분은 제외하고 mcmc 샘플링 함수를 구성하는 과정까지만 옮겨보았다. R코드 위주로만 정리했기 때문에 MCMC에 대한 구체적인 내용을 살펴보고 싶다면 원본 게시물과 다른 자료들을 참고하시길!
library(ggplot2)
library(dplyr)
1. 데이터 생성
표준 정규분포를 따르는 변수 100개를 생성한다
set.seed(123)
data = rnorm(100)
df_data = data.frame(x = data)
생성한 데이터의 분포를 히스토그램을 통해 확인해보자
df_data %>%
ggplot(aes(x = data)) +
geom_histogram(bins = 8, fill='steelblue') +
xlim(-3, 3) +
ggtitle('Histogram of observed data')
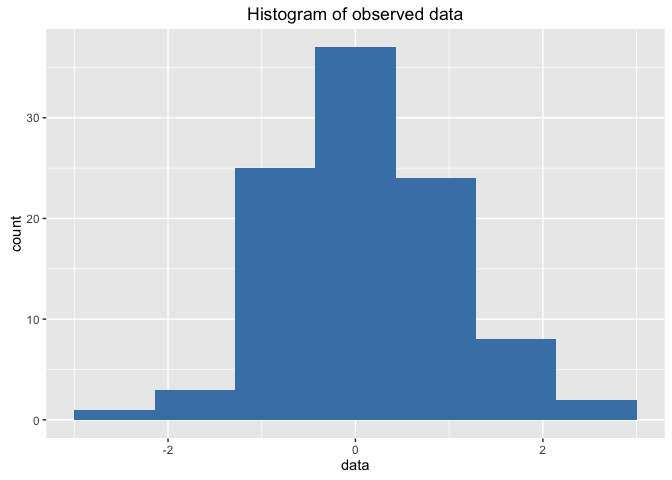
이제 평균의 posterior분포를 찾아보자. 표준편차는 1이라는 것을 알고있다고 가정한다
우선 이론적으로 prior가 정규분포일때의 posterior는 동일하게 정규분포를 따른다
https://en.wikipedia.org/wiki/Conjugate_prior 에서 Normal with known variance의 Posterior hyperparameters를 참고하여 함수를 작성한다
calc_post_analytical = function(data, x, mu_0, sigma_0){
sigma = 1
n = length(data)
mu_post_u = mu_0 / (sigma_0^2) + sum(x) / (sigma^2)
mu_post_l = (1 / (sigma_0)^2) + (n / (sigma^2))
# posterior mean, sigma
mu_post = mu_post_u / mu_post_l
sigma_post = mu_post_l ^ (-1/2)
# (Analytical) posterior density plot
post_x = x
post_y = dnorm(post_x, mu_post, sigma_post)
post_df = data.frame(
x = post_x,
y = post_y
)
result = list(
# posterior parameter
param = c(mu_post, sigma_post),
# sample data for posterior pdf
post_data = post_df,
# posterior pdf by ggplot2
pdf = ggplot(post_df, aes(x=x, y=y)) +
geom_line(colour = 'steelblue') +
ggtitle('Analytical Posterior')
)
# add names to result$param
names(result$param) = c('mu_post', 'sigma_post')
return(result)
}
이제 위에서 생성했던 데이터를 바탕으로 이론적인 posterior를 구할 수 있다
post_analytical = calc_post_analytical(data, seq(-1,1, length.out = 500), 0, 1)
calc_post_analytical함수의 결과물은 세 가지 항목을 가진다.
- Posterior의 평균과 표준편차
- posterior 분포 데이터
- posterior 분포의 ggplot2 그래프
# mu_post , sigma_post
post_analytical$param
## mu_post sigma_post
## -4.012192e-16 9.950372e-02
head(post_analytical$post_data)
## x y
## 1 -1.0000000 4.690287e-22
## 2 -0.9959920 7.025119e-22
## 3 -0.9919840 1.050518e-21
## 4 -0.9879760 1.568369e-21
## 5 -0.9839679 2.337699e-21
## 6 -0.9799599 3.478759e-21
# Analytical Posterior
post_analytical$pdf
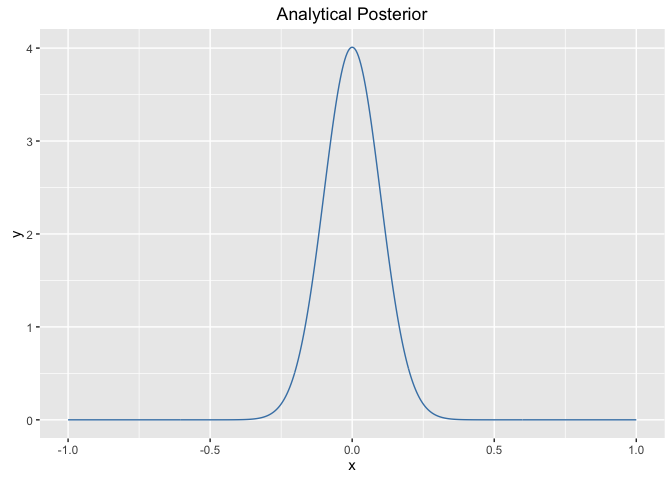
2. MCMC Sampling
MCMC를 통해 샘플링하는 과정을 단계별로 나누어서 살펴보자.
1 Set starting position
MCMC sampling을 진행하려면 먼저 초기값을 설정해야 한다. 여기서 초기값은 임의의 값으로 두어도 괜찮다. 일단은 값을 1로 두고 시작해보자
mu_current = 1
2 Make Proposal
이제 기존에 있던 위치에서 다른 곳으로 옮겨갈수도 있다. 현재 mu값(mu_current)을 중심으로 하는 정규분포를 가정하고 옮겨갈 위치를 제안할 수 있다. 이 때 표준편차는 proposal_width라는 변수로 정의해서 이동 범위를 정할 수 있다
proposal_width = 0.5
set.seed(123)
mu_proposal = rnorm(1, mu_current, proposal_width)
이번에는 제안한 지점이 옮겨갈만한 곳인지 판단해야 한다. 새로 제안한 mu값을 바탕으로 한 분포가 기존 분포보다 데이터를 더 잘 설명한다면, 옮겨가도 좋을 것이다. 현재 지점과 옮겨갈 지점의 prior probability와 likelihood를 구하고 두 값을 곱해서 비교한다(Bayes정리의 분자 부분)
likelihood_current = dnorm(data, mu_current, 1)
likelihood_proposal = dnorm(data, mu_proposal, 1)
mu_prior_mu = 0
mu_prior_sd = 1
prior_current = dnorm(mu_current, mu_prior_mu, mu_prior_sd)
prior_proposal = dnorm(mu_proposal, mu_prior_mu, mu_prior_sd)
# Bayes정리의 분자부분
p_current = prior_current * prod(likelihood_current)
p_proposal = prior_proposal * prod(likelihood_proposal)
3 Accept / Reject the proposal
이제 두 값을 나눈다!
p_accept = p_proposal / p_current
0부터 1사이의 값을 가지는 난수를 하나 발생시키고 p_accept값과 비교한다. 따라서 p_proposal이 p_current보다 값이 큰 경우에는 제안이 무조건 받아들여진다. 현재 parameter의 확률이 더 높은 경우에는 일정 확률로 제안을 받아들인다.
set.seed(123)
accept = runif(1) < p_accept
제안을 받아들이는 경우 해당 값을 현재 값으로 변경한다. 그리고 이 과정을 반복한다
if(accept){
mu_current = mu_proposal
}
이러한 과정을 통해 Posterior 분포에 대한 샘플링 결과물을 얻을 수 있다. 샘플링 과정을 하나의 함수로 구성해보자
sampler = function(data, n_sample = 4, mu_init = 0.5, proposal_width = 0.5,
mu_prior_mu = 0, mu_prior_sd = 1, seed = NA){
# 난수의 seed값이 필요하다면 여기서 지정한다
if(!is.na(seed)){
set.seed(seed)
}
# 초기값을 설정한다
mu_current = mu_init
posterior_result = data.frame(posterior = mu_current,
mu_current = mu_current,
mu_proposal = NA,
p_current = NA,
p_proposal = NA,
accept = NA)
for(idx in 1:n_sample){
# 새로운 mu값을 제안한다
mu_proposal = rnorm(1, mu_current, proposal_width)
# 각 mu별로 likelihood를 계산한다
likelihood_current = dnorm(data, mu_current, 1)
likelihood_proposal = dnorm(data, mu_proposal, 1)
# prior probability를 계산한다
mu_prior_mu = 0
mu_prior_sd = 1
prior_current = dnorm(mu_current, mu_prior_mu, mu_prior_sd)
prior_proposal = dnorm(mu_proposal, mu_prior_mu, mu_prior_sd)
# 두 가지 값을 곱한다 (베이즈 정리의 분자값)
p_current = prior_current * prod(likelihood_current)
p_proposal = prior_proposal * prod(likelihood_proposal)
# 새로 제안한 값의 확률이 더 크다면 바로 채택
# 기존 값의 확률이 더 크다면 난수를 하나 더 뽑아서 해당 값보다 높으면 채택
p_accept = p_proposal / p_current
accept = runif(1) < p_accept
# 채택되었다면 해당 값을 mu_current로 설정하고 이 과정을 반복한다
if(accept){
proposal_df = data.frame(posterior = mu_proposal,
mu_current = mu_current,
mu_proposal = mu_proposal,
p_current = p_current,
p_proposal = p_proposal,
accept = accept)
mu_current = mu_proposal
} else {
proposal_df = data.frame(posterior = mu_current,
mu_current = mu_current,
mu_proposal = mu_proposal,
p_current = p_current,
p_proposal = p_proposal,
accept = accept)
}
posterior_result = rbind(posterior_result, proposal_df)
}
return(posterior_result)
}
샘플링 결과물을 확인해보자
mcmc_result = sampler(data, n_sample = 5000, seed = 123)
head(mcmc_result, n=10)
## posterior mu_current mu_proposal p_current p_proposal accept
## 1 0.5000000 0.5000000 NA NA NA NA
## 2 0.2197622 0.5000000 0.2197622 1.208153e-62 2.544422e-59 TRUE
## 3 0.2197622 0.2197622 0.8148655 2.544422e-59 1.731611e-70 FALSE
## 4 0.2550164 0.2197622 0.2550164 2.544422e-59 1.502840e-59 TRUE
## 5 0.2005334 0.2550164 0.2005334 1.502840e-59 3.216178e-59 TRUE
## 6 0.2005334 0.2005334 0.4309915 3.216178e-59 1.660419e-61 FALSE
## 7 0.2005334 0.2005334 0.8408108 3.216178e-59 2.501439e-71 FALSE
## 8 -0.0222976 0.2005334 -0.0222976 3.216178e-59 3.187863e-59 TRUE
## 9 -0.0222976 -0.0222976 0.2296086 3.187863e-59 2.224370e-59 FALSE
## 10 0.1780881 -0.0222976 0.1780881 3.187863e-59 4.032705e-59 TRUE
샘플링 결과물의 trace는 아래와 같이 확인할 수 있다
mcmc_result %>%
mutate(idx = row_number()) %>%
ggplot(aes(x=idx, y=posterior))+
geom_line(colour = 'steelblue') +
ggtitle('Trace of posterior samples')

초기값은 0.5였지만 점차 0 ~ 0.2 사이의 값으로 안정화되는 모습을 보인다
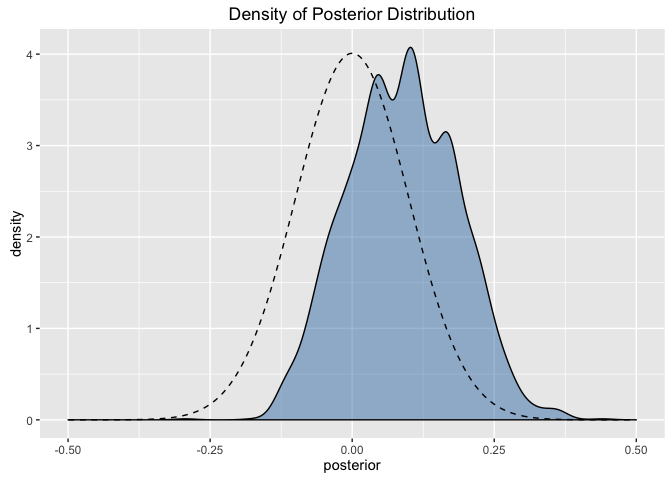
posterior mu 값의 분포를 구하고 위에서 구했던 이론적인 값의 분포와 비교해보자. 그래프에서 점선으로 표시된 분포가 이론적인 계산을 통해 구한 posterior 분포이다.
mcmc_result[3001:5000,] %>%
ggplot(aes(x = posterior)) +
geom_density(fill= 'steelblue', alpha = 0.5) +
geom_line(data = post_analytical$post_data,
aes(x=x, y=y),
linetype = 2) +
xlim(-0.5, 0.5) +
ggtitle('Density of Posterior Distribution')